什么是并查集
（百度：你就这么直接复制吗？，，）在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中，其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。
并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。
操作
大体上有三个
初始化
即最开始每个点都要指向自己（这里有一个要点，因为形成的树每个点都指向他的上家，因而最终只有根节点是自己指向自己；后面的程序便是通过是否指向自己来判断是否为根节点）
for(int i=1;i<=n;i++)
pre[i]=i;//使每一个点都指向自己
查找
首先明确一点，并查集通过判断两个元素所在的树的根节点是否相同来判断这两个元素是否在同一集合。
那么再根据”只有根节点的上家指向自己“这一性质，我们不难码出以下代码
int find(int x)
{
int r=x;//先将当前位置记录
while(pre[r]!=r)//如果不是根节点
r=pre[r];//继续向上家寻找
return r;
}
合并
这个操作很简单，先判断两个元素是否在同一集合中（即所在树的根节点是否相同），如果不在，再将其中一个根节点指向另一根节点。
- 因而也称根节点为一个集合的代表元素
void join(int x,int y)
{
int a=find(x),b=find(y);//将两个元素根节点记录
if(a!=b)//如果不在一个集合（根节点不一样）
pre[a]=b;//将其中一个根节点指向另一根节点
}
实现与优化
那么综合以上的信息，我们可以得到完整代码
//模板 并查集
#include <bits/stdc++.h>
using namespace std;
int pre[10001];
int findd(int x)//因为头文件中包含find函数，所以命名为findd（看个人习惯）
{
int r=x;//先将当前位置记录
while(pre[r]!=r)//如果不是根节点
r=pre[r];//继续向上家寻找
return r;
}
void join(int x,int y)
{
int a=findd(x),b=findd(y);//将两个元素根节点记录
if(a!=b)//如果不在一个集合（根节点不一样）
pre[a]=b;//将其中一个根节点指向另一根节点
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
pre[i]=i;
for(int i=1;i<=m;i++)
{
int k,a,b;
cin>>k>>a>>b;
if(k==1)
join(a,b);
else
if(findd(a)==findd(b))
cout<<"Y"<<endl;
else
cout<<"N"<<endl;
}
return 0;
}
好吧，当你提交这个代码的时候，可能会有一些不太理想的结果，，比如，TLE
这又是为什么呢？
大神指出，每当进行一次查询操作时，都必须从该节点到根节点遍历一次，这意味着，如果一个点距根节点要走1000条边，那每查询一次这个点所在的集合，就要把这1000条边走一次。对此，该大神还提出了一个优化，也就是——————路径压缩
具体就是记录根节点的值后，将这条路径上所有点的上家指向根节点，使之前要走几千步的循环现在只需要进行几次。代码实现如下（这是用循环实现的，还可用递归实现，但就不在这里阐述了）
//优化后的findd
int findd(int x)
{
int r=x;
while(pre[r]!=r)
r=pre[r];
//路径压缩
int i=x,j;//i记录当前点，j记录i的上家
while(i!=r)//若当前点不为根节点
{
j=pre[i];//记录上家
pre[i]=r;//使当前点直接指向根节点
i=j;//当前点移动到上家
}
return r;
}
如果还有不懂的，可以看一下下面这张图
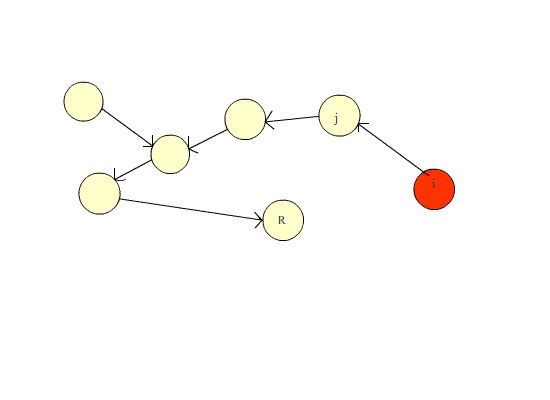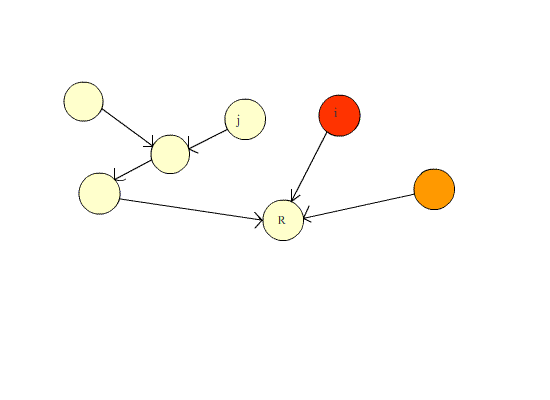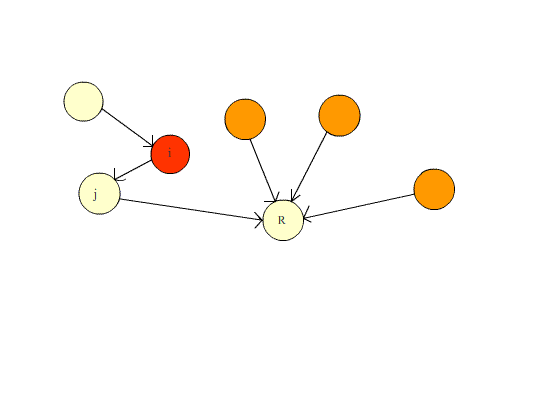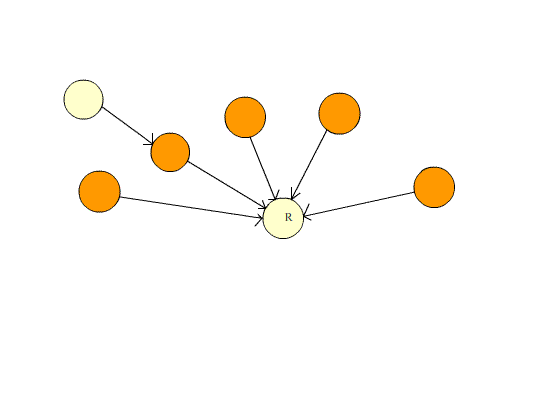路径压缩前，从最右边的点查询根节点需要五次循环，
而路径压缩后，从最右边的点查询根节点只需要一次！！
那么完整代码如下
//模板 并查集 已优化
#include <bits/stdc++.h>
using namespace std;
int pre[10001];
int findd(int x)
{
int r=x;
while(pre[r]!=r)
r=pre[r];
//路径压缩
int i=x,j;//i记录当前点，j记录i的上家
while(i!=r)//若当前点不为根节点
{
j=pre[i];//记录上家
pre[i]=r;//使当前点直接指向根节点
i=j;//当前点移动到上家
}
return r;
}
void join(int x,int y)
{
int a=findd(x),b=findd(y);//将两个元素根节点记录
if(a!=b)//如果不在一个集合（根节点不一样）
pre[a]=b;//将其中一个根节点指向另一根节点
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
pre[i]=i;
for(int i=1;i<=m;i++)
{
int k,a,b;
cin>>k>>a>>b;
if(k==1)
join(a,b);
else
if(findd(a)==findd(b))
cout<<"Y"<<endl;
else
cout<<"N"<<endl;
}
return 0;
}
